Avl Tree Search C++
AVL tree is a self-balancing binary search tree in which each node maintains an extra information called as balance factor whose value is either -1 0 or 1. AVL trees have self-balancing capabilities.
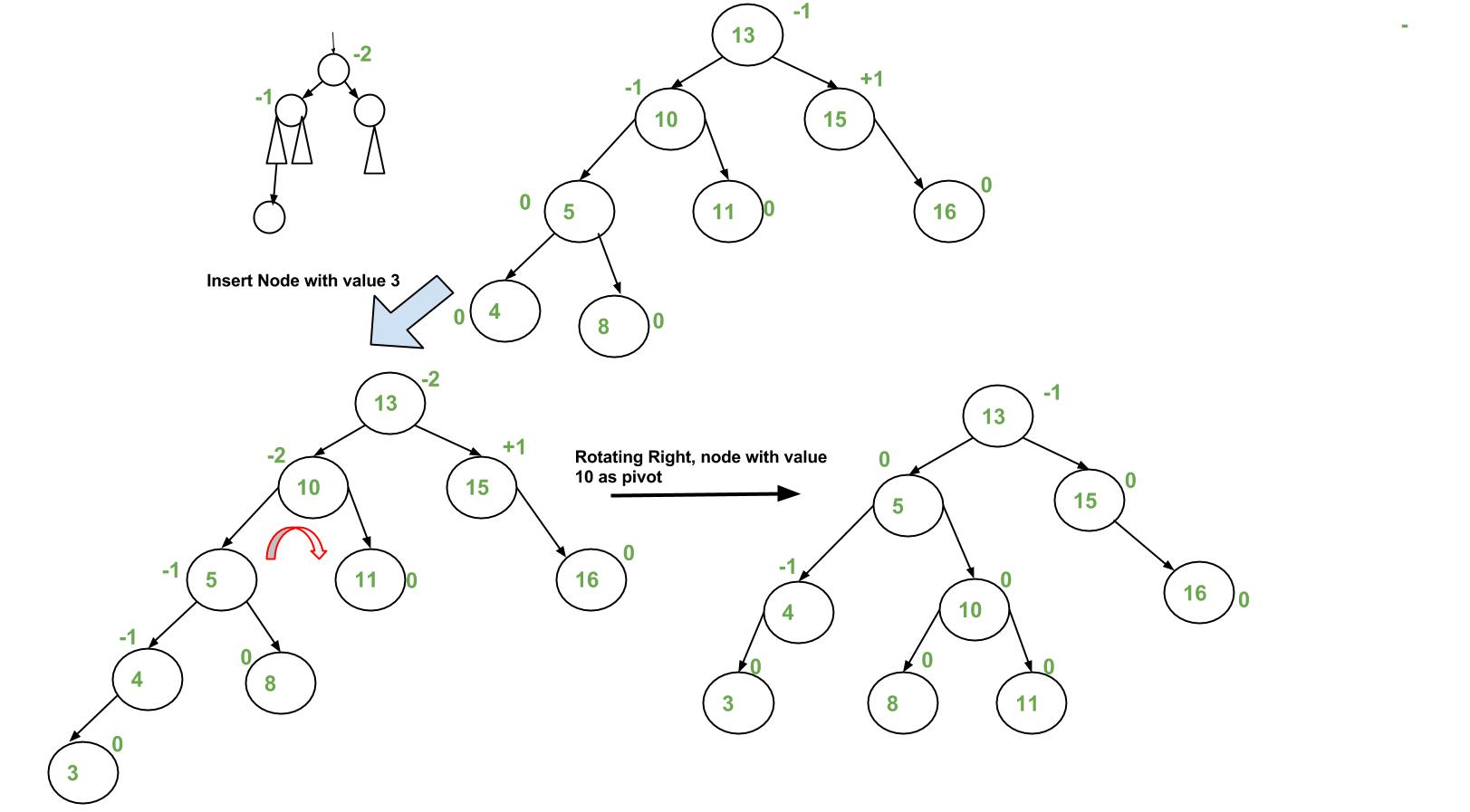
Avl Tree Set 1 Insertion Geeksforgeeks
It requires 1 bit of color information for each node in the tree.

. So time complexity of AVL delete is OLog n. A Binary Search Tree or BST as it is popularly called is a binary tree that fulfills the following conditions. Advantages Of AVL Trees.
There are two standard methods of traversals. It is always height balanced. When the Tree is modified a new tree is subsequently rearranged and repainted.
If this is false then perform this operation recursively with the right sub-tree of the root. Advantages of AVL Trees. In this tutorial you will understand the working of various operations of an avl-black tree with working code in C C Java and Python.
The time required to search a node in BST is more than the balanced binary search tree as a balanced binary search tree contains a lesser number of levels than the BST. AVL trees have efficient search time complexity. The height of the AVL tree is always balanced.
So the time complexity of AVL delete remains same as BST delete which is Oh where h is height of the tree. The binary tree on the right isnt a binary search tree because the right subtree of the node 3 contains a value smaller than it. IF TREE NULL Allocate memory for TREE SET TREE - DATA ITEM.
AVL trees are self-balancing binary search trees. Else check if the item is less than the root element of the tree if this is true then recursively perform this operation with the left of the root. There are two basic operations that you can perform on a binary search tree.
Detailed Tutorial on Binary Search Tree BST In C Including Operations C Implementation Advantages and Example Programs. Since AVL tree is balanced the height is OLogn. It gives better search time complexity when compared to simple Binary Search trees.
The time complexity of the AVL tree is faster and constant in comparison to the binary search tree. The overall cost of searching a node should be less. Constraints maintained by Red Black Tree.
Traversal is the technique using which we visit each and every node of the graph or a tree. Insert TREE ITEM Step 1. AVL tree is a height-balanced tree and therefore the height of the tree never grows more than N where N is the number of nodes in the tree.
Self-Balancing is provided by painting each node with two colorsRed or Black. The nodes that are lesser than the root node which is placed as left children of the BST. The height never grows beyond log N where N is the total number of nodes in the tree.
There is one way that can reduce the cost of a binary search tree is known as an optimal binary search tree. This explicit C tutorial will give you a detailed explanation of traversal techniques that can be performed on a tree or graph. A tree having a right subtree with one value smaller than the root is shown to demonstrate that it is not a valid binary search tree.
Breadth-first searchBFS Depth-first searchDFS. Updating the height and getting the balance factor also take constant time. AVL tree has capabilities of self-balancing.
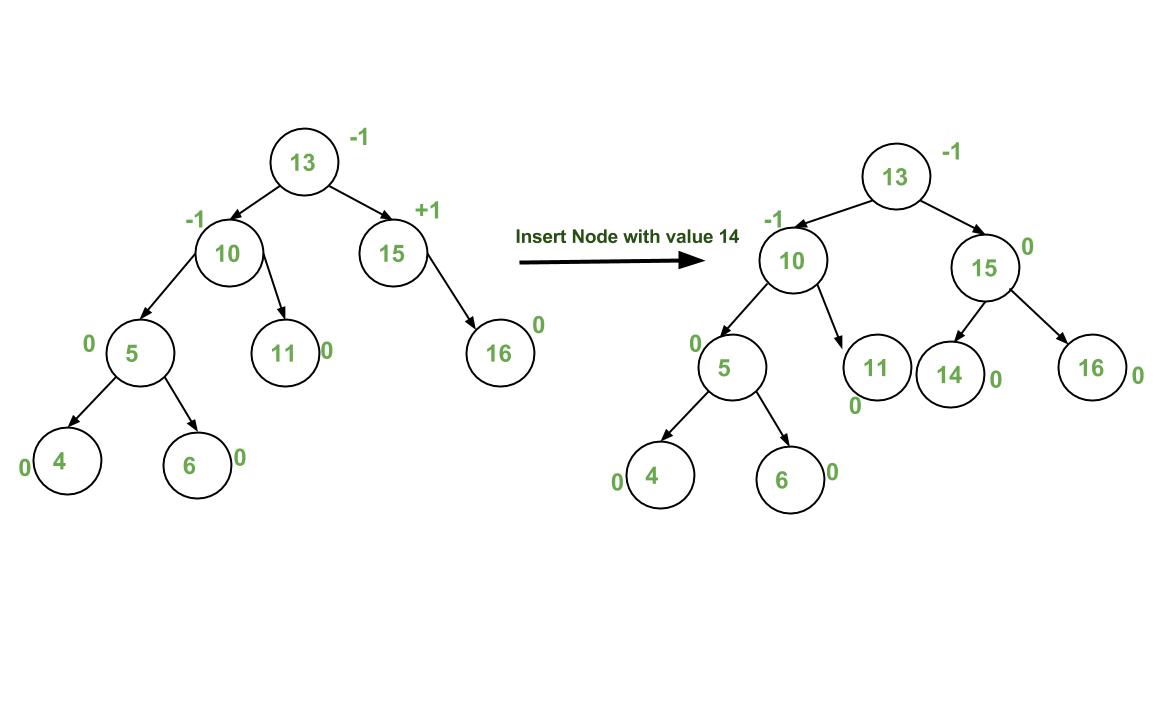
Avl Tree Set 1 Insertion Geeksforgeeks

Avl Tree Set 1 Insertion Geeksforgeeks
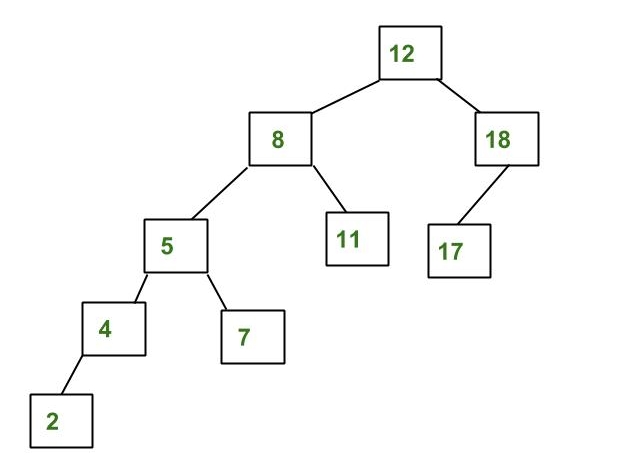
Avl Tree Set 1 Insertion Geeksforgeeks
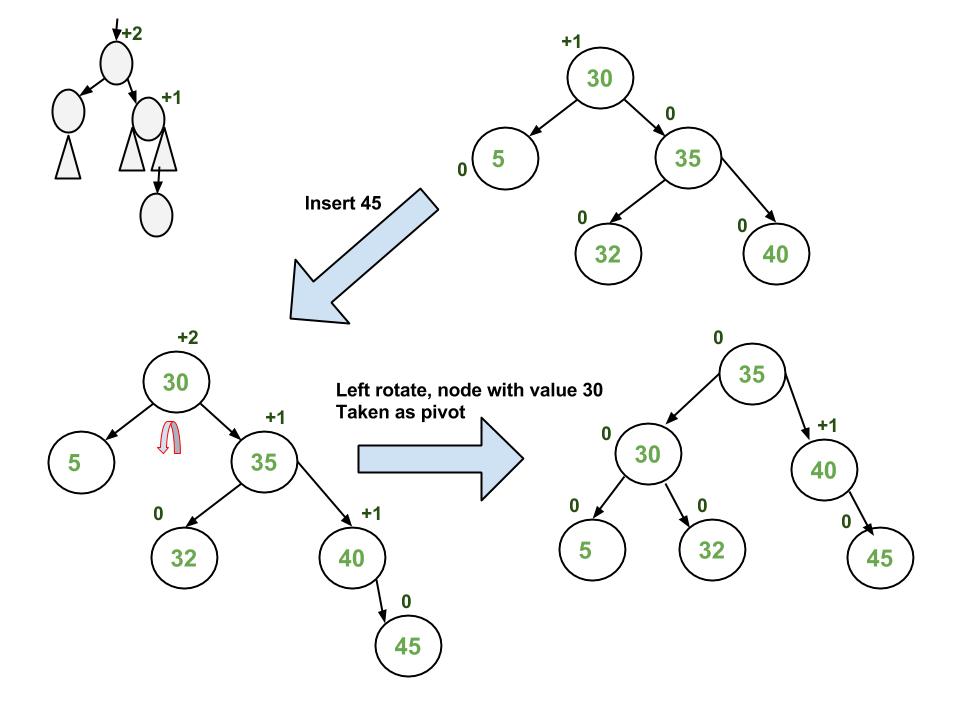
Avl Tree Set 1 Insertion Geeksforgeeks
0 Response to "Avl Tree Search C++"
Post a Comment